|
Ziel beim folgenden Test ist, durch Lösen möglichst vieler Knobelaufgaben möglichst viele Punkte zu erzielen. Dabei geben Level-1-Aufgaben 1 Punkt, Level-2-Aufgaben 2 Punkte, usw.
Eine Zeitbegrenzung gibt es nicht.
Man gebe Lösungsvorschläge erst dann bei mir ab (oder schicke sie hierhin), wenn man sicher ist, keine weitere Aufgabe mehr zu schaffen.
Veröffentlichen darf ich die Lösungen nicht, denn:
Der Test wurde in Brasilien als IQ-Test für Hochbegabte entwickelt (zum Original-Test hier). Nach jüngsten Schätzungen der Autoren kann nur einer von 2330 Erwachsenen die ersten 25 Aufgaben sämtlich lösen. Wer“s schafft, hätte demnach einen IQ von 150, sofern die Intelligenz normalverteilt ist (Median 100, Standardabweichung 15) und von diesem Test tatsächlich gemessen wird (woran man zweifeln darf).
Die ersten 25 (von 36) Knobelaufgaben des Sigma-Tests
Level I
1) 1979 war Marcelo 11 Jahre alt. Wie alt ist er 2002?
2) Wenn 13 Kugeln 3,90 € kosten, wie viel kosten dann 31 Kugeln?
3) Eine Kiste misst 60 cm x 50 cm x 30 cm. Welche maximale Anzahl kleinerer Kisten mit den Maßen 10 cm x 10 cm x 10 cm passt in die große hinein?
4) 12 Personen erledigen eine Arbeit in 12 Tagen. Wie viele Personen schaffen die gleiche Arbeit an einem einzigen Tag?
5) Eine Enzyklopädie umfasst 12 Bände. Jeder Band hat 300 Seiten mit 50 Zeilen auf jeder Seite und 100 Buchstaben in jeder Zeile. Wie viele Buchstaben enthält die gesamte Enzyklopädie?
Level II
6) Ein Betrieb hat Vorräte, um eine Kundschaft von 2500 Personen 12 Monate lang zu beliefern. Wie lange würden diese Vorräte reichen, wenn die Kundschaft auf 6000 Personen anwüchse?
7) Wenn ein Pferd 600 kg ziehen kann, wie viele Pferde braucht man dann für 6150 kg?
8) Fernanda und Andreia sind zusammen 18 Jahre alt. Wie alt ist Andreia, wenn sie doppelt so alt ist wie Fernanda?
Level III
9) Ricardo wiegt 30% mehr als José. Wenn Ricardo 10% seines Gewichts verlöre und José um 20% zunähme, wer wäre dann schwerer? Begründe.
10) Ein Astronom entdeckt ein Sonnensystem. Um den Zentralstern kreisen neun Planeten. Jeder hat 7 Monde. Unter 21 Monden findet sich immer genau einer, um den drei "Unter-Monde" kreisen. Wie viele Himmelskörper hat dieses Sonnensystem insgesamt?
11) Auf einer Treppe liegt Gold, und zwar 1 Gramm auf der ersten Stufe, 2 Gramm auf der zweiten, usw., bis 1 Kilogramm auf der letzten Stufe. Wenn 1 Gramm Gold 11 € kostet, welchen Wert hat dann das gesamte Gold auf der Treppe?
Na, wollen wir die Gehirnwindungen vor den großen Aufgaben nochmal entspannen? Dann bloß nicht
hier klicken! |

|
Level IV
12) 99% der Personen in einem Raum sind Männer. Wie viele Männer müssten den Raum verlassen, damit dieser Anteil auf 98% sinkt? Im Raum befinden sich drei Frauen.
13) Auf einem Schachbrett mit 64 Feldern (8 x 8) können zwei Könige 3612 verschiedene Stellungen einnehmen. Wie viele verschiedene Stellungen können zwei Könige auf einem Schachbrett mit 117 Feldern (13 x 9) einnehmen? Die Könige dürfen niemals auf demselben Feld stehen und auch nicht auf zwei benachbarten Feldern.
14) Marcelo hat Äpfel, von denen er die Hälfte seinem Bruder schenkt. Letzterer gibt 75% der Äpfel seinen Cousins Anderson, Joao und Mané, mit der Bitte, sie gerecht zu teilen. Anderson kauft sich dann noch 7 Äpfel mehr und gibt diesmal die Hälfte seiner Äpfel an Mané. Der hat schließlich 17 Äpfel. Wie viele Äpfel hat Joao?
15) Maria holt Eier vom Bauern. Zu Hause gibt sie die Hälfte ihrer Schwester, welche wiederum ein Drittel dieser Eier an ihren Freund weitergibt. Letzterer isst ein Drittel seiner Eier und reicht den Rest an seine Cousine weiter. Wenn jedes Ei 70 Gramm wiegt und Maria nicht mehr als 2,5 kg tragen kann, wie viele Eier erhält dann die Cousine von Marias Schwesters Freund?
16) Bürgermeister Joao und ein wichtiger Geschäftsmann namens José geben eine große Grillparty. Abgesehen von José (der Geschäftsmann ist Junggeselle), Joao und seiner Ehefrau ist die Anzahl der übrigen Anwesenden genau gleich hoch wie die Anzahl der 100 € -Scheine, die der Bürgermeister aufwendete, multipliziert mit der Anzahl der 100 € -Scheine, die der Geschäftsmann investieren musste. Im Schnitt verbraucht jeder Anwesende (einschließlich José, Joao und seiner Frau) Speisen und Getränke im Wert von 6,40 €. Wie hoch waren die Kosten für den Geschäftsmann, wenn der Bürgermeister 1700 € bezahlt hat?
Level V
17) Ein Formel-1-Wagen umrundet einen Kurs in drei Minuten bei einer Durchschnittsgeschwindigkeit von 144 km/h. In welcher Zeit muss eine zweite Runde zurückgelegt werden, damit die Durchschnittsgeschwindigkeit, gemessen über beide Runden, auf 300 km/h steigt?
18) Als Antonio auf seine Uhr sieht, bemerkt er, dass der Minutenzeiger genau über dem Stundenzeiger liegt. Wie lange dauert es, bis das wieder passiert? (Beide Zeiger bewegen sich gleichmäßig.)
19) Ein Zug mit zwei Waggons fährt mit 80 km/h von Ort X nach Ort Y, die 800 km voneinander entfernt liegen. Im Moment der Abfahrt beginnt ein Fahrgast, in Waggon B von einem Ende zum anderen und zurück zu laufen, mit einer Geschwindigkeit von 100 cm/s. Bei der Ankunft in Ort Y hat der Fahrgast bereits 720 komplette Hin- und Rückwege hinter sich. Die Länge von Waggon A ist die von Waggon B plus ein Viertel der Länge der Lokomotive, und die Länge der Lokomotive entspricht der Länge von Waggon A plus einem Fünftel der Länge von Waggon B. Wie lang ist der Zug insgesamt?
Level VI
20) Mehrere Pumpen füllen sechs Tanks. Eine Stunde lang pumpen sie Wasser in ein Reservoir, von wo aus es zu gleichen Teilen auf die Tanks A, B, C und D verteilt wird. Danach befüllen die Pumpen eine Stunde lang einen Doppeltrichter, der eine Hälfte des Wassers auf E und F verteilt, die andere aber in das Reservoir leitet, so dass diese Hälfte wieder in den Tanks A, B, C und D landet, die damit randvoll werden. Um auch E und F zu füllen, wird nur eine Pumpe betrieben, die zwei Stunden lang ihr Wasser gleichmäßig auf E und F verteilt. Nun sind alle Tanks voll. Wie viele Pumpen sind am Anfang benutzt worden? (die Strömungsleistungen aller Pumpen sind gleich, ebenso die Tankinhalte)
21) Mehrere Rechtecke werden so auf eine ebene Fläche gezeichnet, dass ihre Schnittlinien 18.769 nicht weiter unterteilte Gebiete umschließen. Welche Mindestanzahl von Rechtecken ist hierzu nötig?
22) Mehrere Geraden werden so über eine begrenzte ebene Fläche gelegt, dass ihre Schnitte diese Fläche in 1597 nicht weiter unterteilte Gebiete zerlegen. Welche Mindestanzahl von Geraden ist hierzu nötig?
23) 1 + 101.234.567.890 Dreiecke werden auf eine ebene Fläche gezeichnet. Welche maximale Anzahl nicht weiter unterteilter Gebiete können die sich schneidenden Dreiecke erzeugen?
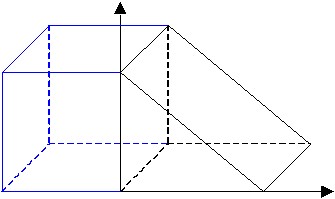
24) Nach der (mittlerweile bewiesenen) FERMATschen Vermutung hat die Gleichung an + bn = cn keine Lösungen für n > 2 (a, b, c und n sollen natürliche Zahlen sein). 1992 fand jemand folgenden einfachen, allerdings fehlerhaften "Beweis": FERMATs Gleichung ist eine Verallgemeinerung des Satzes von PYTHAGORAS, nach dem bei jedem rechtwinkligen Dreieck mit der Hypothenuse c und den Katheten a und b gilt: a2 + b2 = c2 (die Summe der Flächeninhalte der Kathetenquadrate ergibt den Flächeninhalt des Hypothenusenquadrats). Um diesen Satz zu verallgemeinern, gehe man von der zweidimensionalen Fläche zum dreidimensionalen Raum über (a3 + b3 = c3) und betrachte ein Dreiecksprisma. Es wird erzeugt durch die Parallelverschiebung eines rechtwinkligen Dreiecks entlang einer Senkrechte zur Dreiecksfläche (vgl. Bild unten). Je nach Weite dieser Verschiebung ist es möglich aus jeder der drei Seitenflächen des Prismas ein Quadrat zu machen, auf dem dann ein Würfel zu errichten wäre. Leider ist dann aber mindestens eine der übrigen Seitenflächen ein nichtquadratisches Rechteck. Also ließe sich auf dieser Seitenfläche auch kein Würfel errichten. Folglich existiert keine zum Satz des PYTHAGORAS analoge Konstruktion in drei Dimensionen, die Gleichung an + bn = cn hat für n = 3 keine Lösung. Mit einer entsprechenden Schlussfolge könnte man dies für alle n > 2 zeigen. Wo liegen die Irrtümer dieses "Beweises"?
Level VII
25) Ein Getriebesystem bestehe aus 5 konzentrischen Scheiben übereinander, A, B, C, D und E. Die Scheiben haben unterschiedliche Größe und unterschiedliche, aber jeweils konstante Drehgeschwindigkeiten. Einige der Scheiben drehen im Uhrzeigersinn, einige anders herum. Jede Scheibe hat auf der Oberseite einen roten Punkt, und anfangs liegen diese 5 Punkte nicht auf einer geraden Linie. Von einem bestimmten Moment an drehen alle Scheiben, jede sofort mit ihrer vollen Geschwindigkeit, ohne Kontakt zwischen den Scheiben. Scheibe A benötigt 7 Minuten für eine volle 360°-Drehung, B 13 Minuten, C 17 Minuten, D 19 Minuten und E 23 Minuten. Nach einer bestimmten Zeit liegen alle 5 roten Punkte genau auf einer Linie. Dieselbe Position hatte Scheibe A bereits 2 Minuten nach dem Start, B 3 Minuten, C 4 Minuten, D 7 Minuten und E 9 Minuten nach dem Start. Wie lange dauerte es vom Start an, bis die Aufreihung der roten Punkte zum ersten Mal geschah?
By the way: Dafür, dass du auf der Schulsieger-Seite schon so weit vorgedrungen bist, darfst du nun auch Kommentare, Änderungswünsche sowie natürlich Lösungen einschicken, und zwar an hallo@schulsieger.de.
|