Knobelaufgaben für Fortgeschrittene:
Der große Eli-Mathewettbewerb
Liebe Gehirnakrobatinnen und Knobelkönige!
Die folgenden Knobelaufgaben haben eine Besonderheit: Sie erfordern nicht mehr als die Mathematik- und Physik-Kenntnisse, die man bis Klasse 9 erwirbt, sind aber trotzdem schwierig zu lösen. Um nicht zu sagen: verteufelt schwierig!
Mit Hilfe dieser Aufgaben ist es daher möglich, in einem unbefristeten, schulinternen Wettbewerb alle Schüler der Klassen 8 bis 12 gegeneinander antreten zu lassen, denn alle haben gleiche Chancen.
Auch externe Schüler dürfen teilnehmen, sogar Lehrer! Mathematiklehrer natürlich außer Konkurrenz.
Man muss nicht alle Aufgaben lösen, um mitzumachen, das wird vermutlich auch kaum jemand schaffen. Wer glaubt, keine weitere Aufgabe mehr lösen zu können, gibt einfach die bis dahin bearbeiteten ab. Es ist ausdrücklich erlaubt, den Knobelaufgaben mit der gesamten Familie zu Leibe zu rücken, nur sollten dann auch alle Beteiligten den Mut haben, das gemeinsame Werk zu unterzeichnen.
Achtung: Mit den Ergebnissen allein sind -- anders als beim Sigma-Test -- keine Lorbeeren zu ernten, nur mit den Lösungswegen! Dafür kann ein guter Ansatz, der nicht ganz zum Ziel führt, schon eine Menge wert sein.
Lösungen können direkt bei Herrn Busboom abgegeben oder an hallo@schulsieger.de geschickt werden.
Preiswürdige Leistungen werden entsprechend belohnt!!
1) Es fängt ganz harmlos an:
Betrachtet man Vielecke, deren Eckpunkte auf den Punkten eines quadratischen Gitters liegen (Abstand benachbarter Gitterlinien = 1) so lässt sich die Flächenmaßzahl A eines jeden solchen Vielecks allein aus der Anzahl R der Randpunkte und der Anzahl I der inneren Punkte berechnen (vgl. Figur unten). Gib die zugehörige Formel an und führe ihre Richtigkeit an einem nicht-konvexen Siebeneck vor.
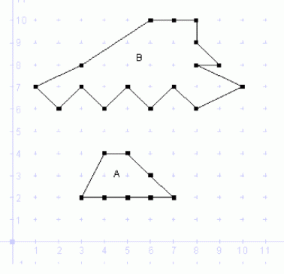
2) Die hier ist schon ganz schön garstig:
Von acht gleich aussehenden Kugeln ist eine schwerer oder leichter als die anderen. Wie kann man mit nur drei Wägungen auf einer Balkenwaage herausfinden, welche es ist und ob sie schwerer oder leichter ist?
3) Gleichungskunst gefragt: Leckerbissen Nr. 16 aus dem Sigma-Test
4) Die richtige Formelgleichung entdecken und auflösen (ab Klasse 9):
Mehrere Geraden werden so durch einen Kreis gelegt, dass ihre Schnitte die Kreisfläche in 1597 nicht weiter unterteilte Gebiete zerlegen. Welche Mindestanzahl von Geraden ist hierzu nötig?
5) Mal etwas ganz anderes (räumliches Vorstellungsvermögen):
Mehrere identische Würfel sind zu einem festen Körper zusammengesetzt. Von diesem Körper sind fünf der sechs Außenansichten gegeben. Die sechste Außenansicht ist in entsprechender Weise zu zeichnen. (eindeutig bis auf Drehungen in der Zeichenebene.)
6) Nur zwei fiese kleine Zahlenfolgen, die man bitte fortsetzen möge:
a) 0 , 6 , 72 , 960 , 15000 , ?
b) 1 , 10 , 5 , 34 , 13 , 74 , ?
7) Dem Glücklichen schlägt keine Stunde:
Günni geht morgens zwischen 7.15 und 7.20 Uhr aus dem Haus. Weil er besonders fleißig arbeitet, schickt ihn die Chefin früher heim. Als er durch die Wohnungstür tritt, fällt sein Blick auf die Wanduhr. Erstaunt stellt er fest, dass Stunden- und Minutenzeiger in der gleichen Stellung stehen wie am Morgen, als er das Haus verließ. Erst glaubt er, die Uhr sei stehen geblieben, dann aber erkennt er, dass die beiden Zeiger ihre Plätze genau getauscht haben. Unter der Voraussetzung, dass sich die Zeiger gleichmäßig bewegen: Wann (auf die Sekunde genau) hat Günni seine Wohnung verlassen und wieder betreten?
8) Wäscheleinen im Quadrat (ab Klasse 9):
Ihr bekommt auf dem Zeltplatz ein quadratisches Stück Rasen zugewiesen, das mit den vier Eckpfosten A, B, C und D markiert ist. Auf dem Rasen liegen drei Wäscheleinenstücke, und Ihr beschließt, diese zwischen den Pfosten zu spannen. Doch leider ist keines der Stücke lang genug, zwischen zwei Pfosten gespannt zu werden. Doch du hast eine schlaue Idee: Ihr knotet die beiden längeren Seile zu einem Kombi-Seil zusammen und bindet dessen Enden um zwei diagonal gegenüberliegende Eckpfosten (B und D). Um das Seil zu spannen, benutzt Ihr das dritte Leinenstück, dessen eines Ende Ihr in Punkt K an das Kombi-Seil knotet und dessen anderes Ende Ihr an Pfosten A befestigt. A ist nun 6 Meter von dem eben erzeugten Knoten K entfernt, der wiederum 10 Meter bzw. 14 Meter Abstand von B bzw. D hat.
Welche Seitenlänge (auf cm genau) hat die Zeltplatzfläche (das Quadrat ABCD)?
9) Vollkommen verblüffend:
Ein Dattelpflücker und Kamelbesitzer hat das Leben in seiner kleinen Oase satt. Er hat 3000 Premium-Datteln gepflückt und will sie samt Kamel in der nächsten Stadt auf dem Markt verkaufen, als Startkapital für ein neues Leben. Die Stadt liegt 500 km entfernt, bis zu ihren Toren gibt es unterwegs nichts als Wüstensand. Das Kamel kann maximal 500 Datteln tragen und frisst pro Kilometer Strecke eine Dattel. Er selbst trägt keine Datteln, nur ausreichend Proviant und Wasser für sich. Die Datteln vergammeln und vertrocknen nicht. Wie viele Datteln kann er maximal auf dem Markt verkaufen?
10) Ein Klassiker, der es in sich hat (ab Klasse 9):
Eine 5 m hohe Leiter steht so an eine Wand gelehnt, dass sie die Ecke einer 1 m breiten und 1 m hohen Kiste genau berührt (vgl. Skizze). In welcher Höhe berührt die Leiter die Wand?
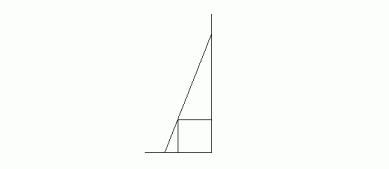
11) Hier ruft ARCHIMEDES nicht "Heureka", hier verzweifelt er:
Eine Schiffsschleuse (Lock) ist 200 Meter lang, 50 Meter breit und 20 Meter tief. Eine quaderförmige Barke in der Schleuse hat 80 Meter Länge, 25 Meter Breite, and 5 Meter Höhe. Sie hat 3000 Fässer giftiger Chemikalien geladen und verdrängt 8000 Tonnen Wasser. Die Dichte des Wassers beträgt eine Tonne pro Kubikmeter. Jedes Fass ist wasserdicht, hat ein Volumen von einem Kubikmeter und eine Masse von zwei Tonnen. Terroristen haben die Funktion der Schleuse sabotiert und eine Zeitbombe an der Barke befestigt, die in drei Stunden zünden wird. Zwar besitzt die Barke einen Aufzug, mit denen sich die Fässer an Deck holen lassen, aber die Crew ist nicht in der Lage, die schweren Fässer rechtzeitig über eine schiefe Ebene an Land zu rollen. Allerdings liegt das Deck nur zehn Zentimeter unterhalb der Dockkante. Könnte man die Barke so weit anheben, ließen sich die Fässer problemlos an Land rollen. Wenn kein Wasser einlassbar ist, wie wiele Fässer müsste man mindestens über Bord rollen, damit die Barke so hoch steigt, dass ihr Deck auf gleicher Höhe oder knapp oberhalb der Dockkante liegt? (vgl. Skizze unten)
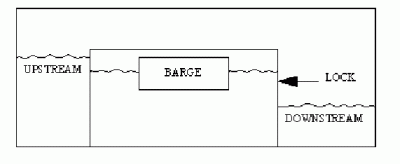
12) Jetzt wird´s ekelig:
Man stelle sich drei Ameisen vor, die jede von einer Ecke eines Dreiecks zur nächsten kriechen. Die Wahrscheinlichkeit, dass sich keine zwei Ameisen dabei begegnen, ist 2/8 (= 1/4), denn nur wenn entweder alle linksherum gehen - LLL - oder alle rechtsherum - RRR, treffen sie sich nicht. In den sechs anderen Fällen - RRL, RLR, RLL, LLR, LRL, and LRR - begegnen sich Ameisen entweder unterwegs oder an einer Zielecke. Nun stelle man sich eine analoge Situation im Räumlichen vor, bei der je eine Ameise auf jeder Ecke eines Würfels sitzt und alle gleichzeitig über eine Kante zu einer benachbarten Ecke marschieren. Wenn alle Ameisen ihren Weg zufällig wählen, wie groß ist dann die Wahrscheinlichkeit, dass sich weder unterwegs noch an einer Zielecke auch nur eine einzige Begegnung ereignet? Man gebe die Lösung als gekürzten Bruch an.
13) Eine echte Grausamkeit: die Nr. 25 aus dem Sigma-Test
14) Und als Krönung: Das hammerharte Weihnachtsrätsel 2001
Z) Zusatzaufgabe für Kettenregel-kundige (ab Klasse 11):
Weise nach, dass der kürzeste Graph, der vier im Quadrat (Seitenlänge a) angeordnete Punkte miteinander verbindet,
nicht etwa die Länge 
(doppelte Diagonale) hat,
sondern vielmehr die Länge 
.
Dieser Graph enspräche z.B. dem kostengünstigsten Straßennetz, das zwischen vier im Quadrat liegenden Orten denkbar ist.